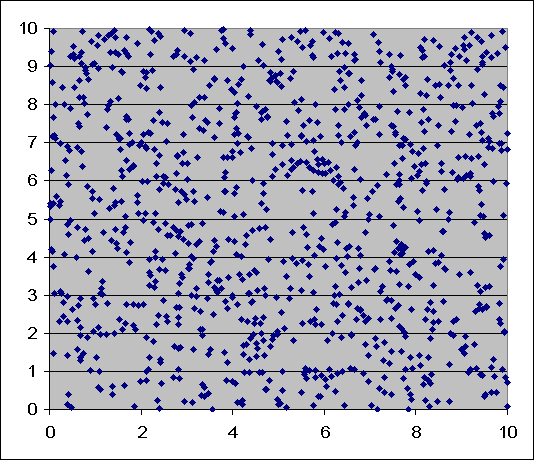
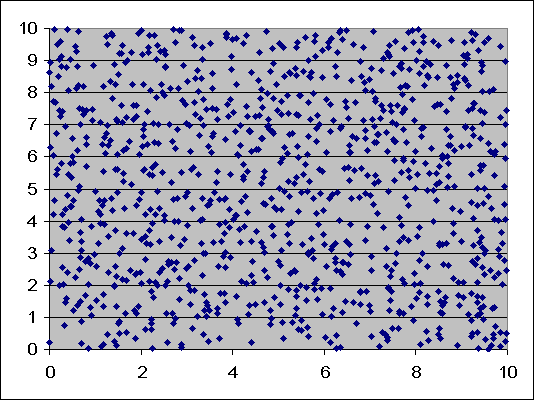
Basically this outlines one of the key notions in statistical analysis. It is very easy, especially for an untrained eye to find patterns in randomness. When we look at the first graph we see patterns, we see little stretches of cluttered dots, some areas where no dots actually appear. If we look hard enough, we can come to some conclusions about what is happening in this graph. If we look at the second graph, we see not a lot of clusters. The dots are very evenly spread and not many big gaps.
An untrained eye would immediately say that the second graph is random, when in fact the opposite is true. The first graph is random. It is very easy to find patterns in randomness. It occurs today in global warming. When we have one of the hottest days on record, or when we have severe storms. We might look at the last couple of years and say that there’s been a drought, or temperatures have increased, there isn’t much rainfall.
But statisticians prove whether this is due to outside causes, or whether this is purely random variation. The only way to do this, is to analyse the data and use statistical tests. This is the only way to prove why we are having changes that we are having now.
Sure we are going to get some hot days, some cold days, some blizzard snow days and some stinking hot days. But is this change in the weather due to global warming? The only way to find out, is not to hypothesise and simply say “it must be, I can’t remember such strange weather” as so many people seem to be doing, but rather analyse the data, see if this strange weather is any different from the norm or if it is purely just random variation.
Only a statistician can prove whether the weather is statistically significantly different now or whether it’s just natural variation. So when an article or scientists tells you that temperatures have significantly increased, or that cycles are more common now that previous, or that temperatures are so cold and warm and everywhere now, ask for a p value. If they don’t have one, or don’t know what you are talking about, then they simply have either not done the research to back up their claims or they, like it seems every other untrained number cruncher, are simply finding patterns in randomness.
19 comments:
Jonathan,
Being neither an academic nor statistician can you explain what you mean by the 'p' value in layman terms? I would be very interested in how this works in the stats.
Keep plugging away.
Cheers
Hi Dazz, a p value is the result after a statistical test to prove one thing or another. the p value represents the probability that the result is due to chance or natural variation. Specifically, if the p value is less than 0.05 (5%) then we generally close a significant difference, in that the difference that has occured is not just due to random variation. If it is above 0.05 then we conclude that there is no evidence to suggest a significant difference.
In other words, temperatures might have increased of late, and decreased at other times, but is this deviation from the norm natural variation or is there a significant difference? A significant difference might indicate for example that humans and CO2 is the cause, or something else. But if there is on significant difference, then well, there is no proof that we are heating up, which is currently the case, as the p values are all above 0.05
"The p value represents the probability that the result is due to chance or natural variation."
No it doesn't. It is the other way around. It represents the probability that, in a hypothetical setting where reality is described by some so-called "null model" according to which there is no trend, you would see a deviation stronger than you've observed.
That deviaton pointing to a trend would then have to be due to pure chance alone. So, the stronger the deviation from the null model, the lower the probability.
This sort of simplisic tests are not the way to detect small subtle effects when you have limited data. You can always assume some null model and then say that you didn't detect a significant deviation from the null model.
If you want to translate your p value to the probability that there is a trend, then you need to know how likely a trend is a priori. This is difficult to estimate. However, this does tell you that it is unfair to take your null model to be something that is regarded to be a priory unlikely.
So, perhaps you should present your results differently. If you take the observed global warming for the Earth as your null model, then how significant is the deviation you have observed?
Or put differently, what is the probability that if Australia is warming as fast as the rest of the Earth, then how unlikely would it be to observe a deviation as large or larger than you've observed?
If that's lower than 0.05, then you do have an important result.
Umm, Count Iblis, you are wrong. It's the other way around. A p value less than 0.05 represents a deviation from the null hypothesis. And it's got nothing to do with a hypothetical reality.
eg a p value of 0.03 proves a significant difference, there is only a 3% chance that the difference is due to chance, and a 97% chance that there is a significant difference. A p value of 0.7 suggests a 70% chance that any deviation is due to chance, and a 30% prob that it isn't. Other way around mate.
"This sort of simplisic tests are not the way to detect small subtle effects when you have limited data."
They are the only way
"You can always assume some null model and then say that you didn't detect a significant deviation from the null model."
Nope wrong there. We are testing if the difference in temperature we may/may not be seeing now is due to natural variation or not. Significance tests is the only way to test this.
"You can always assume some null model and then say that you didn't detect a significant deviation from the null model."
Umm, this is completly the false way to do scientific tests. The null is always that there is no differnce, the alternate is that there is.
I am afraid you are wrong on all counts here Count Iblis, please feel free to read a 1st year statistics book.
Thanks Jonathan. I will stick with your explanation...cheers
Jonathan,
OK..Please tell me to go away and read a book on the subject if you like but I'm enjoying the Stats 101 lesson. I have another question for you. How do you get the 'P' value? I think I understand what you mean but not sure how you get this value.
By the way does the 'P' stand for anything?
Thanks for the lessons!!
Cheers
Utter nonsense Jonathan. This just shows that you don't understand much about the complexity of the problem and therefore your simplistic methods are inappropriate.
I find it shocking that a Ph.D candidate doesn't know the basics of probability theory, in this case Bayes's theorem relating the probability of finding a certain data set given some scenario X and the probability of some scenario X given the data set.
I guess that you've read dumbed down statistic books. In high school we were taught this subject also, but even there we were taught the subtleties of this.
"The null is always that there is no difference"
Well, why not assume a null according to which there is no difference in the incidence of lung cancer and smoking in Angola. No such tests have been done there. Do a small test such that any reasonable effect will fall within your confidence limits. The result will point out that there is no significant increase in the incidence of lung cancer compared to non smokers in Angola.
Now you could dismiss this example as a badly chosen caricature of your work. But let's just take this example as an illustration that you canot reverse the probabilities. The probability that the data is significant according to the null model and the probability that the null model is true are not, in general, simply related.
A null hypothesis that there is no link between lung cancer and smoking in Angola is unreasonable given all the data from the rest of the world. So, one has to do the study the other way around to see if the link betwen lung cancer and smoking is significantly different in Angola than inthe rest of the world.
I suggest you do the same for climate change in Australia. I'm not saying that your data is wrong, or that you've manipulated data. You've just calculated something that is of no interest.
wow wow wow, Count Iblis II, calm down dude. Are we talking about Bayes's theorem or not? Sorry dude, completly different matters.
Please tell me what your credentials are in statistics. Please do. I have a Bsc (hons) and MSc in statistics. According to wikipedia, the root of all correctness (lol!) the p value is "the probability of obtaining a result at least as "impressive" as that obtained, assuming the truth of the null hypothesis that the finding was the result of chance alone."
So you are completly wrong.
"I guess that you've read dumbed down statistic books. In high school..."
LOL LOL LOL LOL LOL LOL LOL LOL LOL. You are saying that your high school knowledge of how statistics works is better than my 9 years at university? please. I encourage you to read a first year university book of statistics before you so make a fool of yourself once again. Sorry, but you really dont want to be making big stuff ups like this again when trying to prove me wrong.
Credentials are irrelevant, Mr. Nobody can publish in Nature if he has the results that merit publication. But anyway, I'm an expert in statistical physics and qauntum field theory. I know a lot about probability theory, but I admit that I don't have a lot of hands on experience with handling huge amounts of data. I've just completed my Ph.D. and I've published 15 articles in peer reviewed journals.
"So you are completly wrong."
No, because credentials are irrelevant, only the results and argumentations count. Prof. Dr. X can be wrong and Mr. Nobody can be right. This is how science works.
"the probability of obtaining a result at least as "impressive" as that obtained, [B]assuming the truth of the null hypothesis[/B] that the finding was the result of chance alone."
That's what I said all along (you assume the null model). In this case, all you've said is that probabilities are not as low as required to rule out a model. But that model is not the favored model that climate scientists assume. Your results would be much more interesting if you turn it around and show that Australia's temperature trend is significantly below that of the global trend. Because then you rule out the standard climate scenario with 95% (or higher) probability, assuming what the climate scientists say is happening for the rest of the world.
That would be a very important result that you can perhaps publish in Nature. Otherwise you have a (literally) insignificant result. You usually cannot conlude very much from the fact that some probability is, say, 0.3 and not as low as 0.05. assuming some model. It is neither strong confirmation of that model (because you started out assuming that model to be true), nor is it evidence that that model is wrong.
It shouldn't be so difficult to subtract from the data you've used the global trend and see if there is a significant downward trend. That could well yield a significant result, in which case I look forward to reading your publication.
Hi Jonathan. Nice site. I'm a statistician too and have been following AGW (and other "Green" issues) for many years.
It's really appalling, isn't it? More than appalling - frightening.
hi Kevin,
wouldn't say that it's appaling, but is a little frightning. It is strange that despite the massive amounts of money being pored into the science, that no-one, and I repeat, no-one, as done a analysis of Australian temperatures that deserve it's warrent.
I would say that is appalling AND frightening, Jonathan. But not surprising in the least. Much basic research has not been done.
There are several reasons for this but I believe one of them is that many Physicists, who dominate climate science, are actually not very good researchers, frankly. In their closed-form world,if the theory (and the models) say something has happened and the data indicate it hasn't, then the data are wrong. So why care about the data?
I don't have it that easy.
Kevin,
I'm a physicist myself and I have to say that you are talking nonsense.
Dear Count iblis,
Sorry if you have taken offense but I stand by my comment that many Physicists are not very good researchers. Indifference to data quality and quantity, inappropriate use or misuse of statistical methods (e.g., linear regression in time-series analysis) are rampant in climate science.
Perhaps outside of climate science my generalization would not hold, and there is an awful lot of awful research being done in other fields, such as medicine.
However, I would add that I have seen what seems to a veteran statistician, if not a climate scientist, as very good work. However, this is the work least likely to see the light of day in media coverage.
Kevin,
There is some truth in what you write. E.g. a Prof. in statistics made similar remarks when he gave a talk on max-ent methods some time ago at our institute
But I think that these things are not so relevant in the fields where physicists work with large amounts of data. Physicists usually do large scale simulations to test all their software before they use it to analyze the data.
E.g. the particle physicists at CERN are busy right now to run simulations of different theoretical scenarios. They have measured the characteristics of their detectors. They simulate the data they would see if a particular theoretical scenario is true and they then let their data analysis software work on that data to see if what comes out is consistent with what they put in.
This is the only practical way to see if there are mistakes in the extremely complicated software.
The huge increase in computer power has made it possible to do away with making simplifying approximations which may cause your results to become biased. You can calculate exactly what you want to calculate from first principles.
Dear Count,
I understand all of this but calculations from first principles are in fact not possible because the first principles are generally not known within the climate system. This would include climate sensitivity to changes in CO2. Very broadly speaking, what I am saying is analogous to the distinction between bivariate analysis and multivariate analysis.
I agree with that. My disagreement with Jonathan is simply that you cannot conclude much from a statistically insignificant result as opposed to a statistically significant result.
You can't say that just because you could not rule out the null model at 95% confidence level in your study that other people who have done another study and have reached another conclusion must be wrong.
You could only say that there is a discrepancy between the two studies if the result of the other study is outside your confidence interval.
So, I like to see confidence intervals from Jonathan, and not just meaningless statements like "no significant change".
Sorry, I became anonymous in my last post by clicking on the wrong button.
I have a number of general concerns about the way statistical inference is used in practice that are relevant to this thread.
1) Classical statistical inference assumes probability sampling. The Australian surface temperature readings in reality come from a convenience sample so, strictly speaking, statistical significance here is meaningless.
2) Even if we choose to ignore 1), as is commonplace in many fields, we must recognize that significance levels are largely a function of sample size. Do we use daily readings, monthy readings, annual temperature readings? This will have a huge impact on our p-value, even if the trends are very similar.
3) Statistical significance is not the same as substantive significance. A highly statistically significant result may in fact result from a large sample size, but may be too small to be of practical significance.
4) The use of linear regression on time-series data is ill-advised. The confidence intervals will be wrong (typically too small) and the slope coefficient is likely to be off as well. Including a linear trend variable in a Box-Jenkins model and forgetting all about statistical significance in this example would be what I would do (though I would duly report my meaningless p-value).
Writing quickly, hope this makes sense.
Hi Jonathan,
You might find the term 'apophenia' to your liking. A propensity to perceive patterns in randomness seems a part of the human condition.
The notion of 'proof' being provided by a blunt statistical test seems a bit much. If an experimenter could manipulate climatic conditions in a representative, controlled fashion -- if there were a handy 'control planet' exactly like Earth, perhaps containing people who acted differently -- that'd work for the task at hand. But statistical tests of hypotheses, and the associated asymptotic theory, are fundamentally mathematical constructs.
My very limited experience with climatological models has been that they are quite complex, and prone to violation of underlying assumptions. This isn't necessarily a bad thing -- if a model gives the right answers at the right times, it's a good model -- but to take the next step and claim a result proven *solely from the result of statistical tests* invites a wide variety of legitimate objections. Not least of which is that the model used to test hypotheses may or may not mirror the underlying climatology.
In short, the type of proof that statisticians are best able to provide is the mathematical sort. Further afield, I don't believe 'proof' is exactly the right word for what we provide. Evidence, surely. But proof?
Post a Comment